Combinatorics is the study of finite structures, many of which arise in other branches of mathematics or from problems arising in science or engineering. The study of combinatorics involves general questions of enumeration and structure, matroid theory and aspects of graph theory, partially ordered sets, set partitions and permutations and combinatorial structures such as finite geometries and designs. Techniques tend to be algebraic and topological, involving methods from commutative ring theory, algebraic topology, representation theory and Hopf algebras.
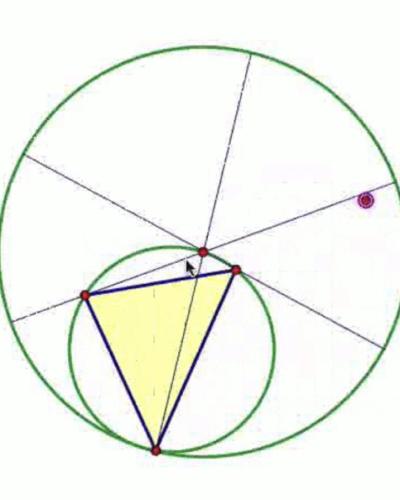
Discrete geometry is concerned with properties of finitely generated geometric objects such as polytopes and polyhedra, triangulations and polyhedral complexes, configurations of lines and, more generally, hyperplanes in Euclidean and other spaces, the theory of rigid and flexible frameworks, tilings and packings. Many problems in discrete geometry arise from questions in computational geometry related to algorithms for analyzing discrete geometric structures.
Faculty Members
| Marcelo Aguiar | Algebra, combinatorics, category theory |
| Robert Connelly | Discrete geometry, computational geometry and the rigidity of discrete structures |
| Tara Holm | Symplectic geometry |
| Jon Kleinberg | Networks and information |
| Robert Kleinberg | Algorithms and theoretical computer science |
| Allen Knutson | Algebraic geometry and algebraic combinatorics |
| Lionel Levine | Probability and combinatorics |
| Karola Meszaros | Algebraic and geometric combinatorics |
| Edward Swartz | Combinatorics, topology, geometry, and commutative algebra |
| Éva Tardos | Algorithm design and algorithmic game theory |
Emeritus and Other Faculty
| Louis Billera | Geometric and algebraic combinatorics |
| Shiliang Gao | Algebraic combinatorics |
| Marie MacDonald | Number Theory, commutative algebra, combinatorial geometry, university mathematics education |
Activities and Resources:
Historically, there have been connections between combinatorics, in particular enumeration theory, and questions in probability. In recent decades, there have been close connections between certain areas of combinatorics and questions arising in theoretical computer science and discrete optimization. Even more recently, there have arisen links to biology, in particular, the study of phylogenetics.
The group at Cornell is particularly interested in algebraic and topological combinatorics, questions of enumeration in polytopes and, more generally, matroids, combinatorial Hopf algebras and rigidity in discrete geometric structures.
